Contoh Alat Peraga SMP dan Cara pembuatannya ; HUBANTSUKA ( Hubungan Antara Sudut Matematika )

HUBANTSUKA (Hubungan Antar Sudut Matematika)

Rizqi Alfian Ardhany

Arman

PROGRAM STUDI PENDIDIKAN MATEMATIKA

FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SILIWANGI

TAHUN 2020

A. Deskrpsi Alat Peraga Matematik

UBANTSUKA adalah singkatan dari Hubungan Antar Sudut Matematika. Media HUBANTSUKA adalah salah satu media pembelajaran matematika yang digunakan untuk membuktikan hubungan di antara sudut-sudut matematika. Sudut-sudut yang akan dibuktikan dari media HUBANTSUKA adalah sudut-sudut yang terbentuk jika terdapat dua buah garis sejajar yang dipotong oleh garis lain, yaitu diantaranya sudut sehadap, sudut sepihak, sudut bersebrangan, dan sudut bertolak belakang.

Komponen yang terdapat di dalam media HUBANTSUKA ialah :

1. Papan yang terdapat dua buah garis sejajar yang dipotong oleh garis lain.

2. Model X yang akan digunakan untuk mengetahui hubungan antar sudut yang saling bertolak belakang.

3. Model F yang akan digunakan untuk mengetahui hubungan antar sudut sehadap.

4. Model Z yang akan digunakan untuk mengetahui hubungan antar sudut bersebrangan.

5. Model C yang akan digunakan untuk membuktikan besar sudut yang sepihak.

Pembahasan

Ø Sudut Sehadap

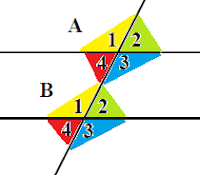
Dikatakan sudut sehadap apabila dua buah garis sejajar dipotong satu garis, maka sudut-sudut sehadap yang terbentuk sama besar.

Ø Sudut Bersebrangan Dalam

Dikatakan bersebrangan dalam, apabila dua buah garis sejajar dipotong oleh suatu garis ketiga, maka sudut sudut yang terbentuk sama besar.

Ø Sudut Bersebrangan Luar

Dikatakan bersebrangan luar apabila dua buah garis sejajar dipotong oleh garis, maka sudut-sudut luar bersebrangan sama besar.

Ø Sudut sepihak

Dikatakan sepihak apabila dua buah garis sejajar dipotong oleh suatu garis, maka sudut-sudut dalam atau luar sepihak jumlahnya .

B. Bahan Yang digunakan untuk membuat alat peraga matematika

Nama Bahan	Kuantitas	Harga
Papan	1	-
Double tip	1	Rp.4.000
Kertas origami	1	Rp.4.000
Karton hitam	1	Rp.4.000
Karton merah	1	Rp.4.000
Kardus bekas	1	-
Lem	1	Rp.10.000
Karton kuning	21	Rp.4.000
Paku mading	1	Rp.5.000

C. Alat yang digunakan untuk membuat alat peraga matematika

Alat yang digunakan untuk membuat alat peraga Hubantsuka ialah :

Ø Gunting

Ø Penggaris

Ø Kater

Ø Alat tulis

(Spidol,pensil,pulpen, dan penghapus)

D. Cara pembuatan alat peraga matematika

Dalam membuat alat peraga Hubantsuka, terdapat beberapa langkah diantaranya :

1. Siapkan alat dan bahan yang telah disediakan.

2. Buatlah tulisan HUBANTSUKA dengan menggunakan kertas origami.

3. Buatlah 3 buah garis dengan menggunakan kertas karton berwarna hitam.

4. Lapisi permukaan 3 buah garis tersebut dengan menggunakan double tip.

5. Siapkan papan dan kertas karton untuk menempelkan ketiga garis tersebut.

6. Potonglah papan dan kertas karton yang telah disiapkan.

7. Lapisi permukaan papan dengan menggunakan lem untuk menempelkan kertas karton tersebut.

8. Tempelkan kertas karton pada papan yang telah dilapisi lem.

9. Tempelkan tulisan HUBANTSUKA dan garis yang telah yang telah dibuat sebelumnya. Garis ditempelkan membentuk 2 garis sejajar yang dipotong oleh garis lain.

10. Buatlah model huruf Z, X, F, dan , C dengan menggunakan cara yang sama.

11. Berikan warna pada setiap model dengan menggunakan kertas origami.

12. Tempelkan garis pada setiap model dengan menggunakan kertas karton hitam dan sesuaikan garis pada papan serta berikan nama pada setiap sudut garis tersebut.

13. Berikan hiasan pada bagian pinggir dari papan media untuk mempercantik tampilan agar lebih menarik.

E. Cara menggunakan alat peraga matematika

Langkah-langkah dalam menggunakan alat peraga Hubantsuka :

1. Model X berfungsi untuk mengetahui hubungan dua sudut yang saling bertolak belakang.

Ø Ambil model X lalu tempelkan pada papan Hubantsuka menggunakan paku. Letakan model sedemikian sehingga garis-garis pada model dan papan Hubantsuka saling berhimpit.

Ø Perhatikan nama-nama sudut pada model.

Ø Model ini akan membuktikan bahwa sudut 1 dan sudut 3 akan saling bertolak belakang dengan cara memutarkan model X searah dengan jarum jam atau berlawanan dengan arah jarum jam.

Ø Lakukan hal yang sama terhadap sudut 2 dan sudut 4.

Ø Maka akan terbukti bahwa sudut 1 dan sudut 3 sama besar serta sudut 2 dan sudut 4 adalah sama besar dan saling bertolak belakang.

2. Model F digunakan untuk mengetahui hubungan dua sudut yang saling sehadap.

Ø Ambil model F lalu tempelkan pada papan Hubantsuka menggunakan paku. Letakkan model sedmikian sehingga garis-garis pada model dan papan Hubantsuka saling berhimpit.

Ø Perhatikan nama-nama sudut pada model.

Ø Geserkan model F ke atas tanpa melawan garis hitam pada papan Hubantsuka.

Ø Kemudian tempelkan kembali model F pada tempat semula. Kemudian putar searah atau berlawanan arah jarum jam sebesar . Maka dapat dilihat bahwa sudut sehadap adalah sama besar.

Ø Lakukan hal yang sama terhadap sudut yang lainnya.

3. Model Z digunakan untuk mengetahui jumlah sudut yang saling bersebrangan baik dalam maupun luar.

Ø Ambil model Z lalu tempelkan pada papan Hubantsuka menggunakan paku. Letakkan model sedmikian sehingga garis-garis pada model dan papan Hubantsuka saling berhimpit.

Ø Perhatikan nama-nama sudut pada papan model Z.

Ø Untuk membuktikan sudut bersebrangan luar, perhatikan sudut-sudut diluar model Z.

Ø Kemuadian putar model Z searah atau berlawanan arah jarum jam sebesar maka akan terlihat sudut yang saling bersebrangan.

Ø Lakukan hal yang sama pada model Z jika ingin mengetahui sudut bersebrangan dalamnya. Namun perlu diperhatikan sudut mana saja yang termasuk sudut dalam bersebrangan.

Ø Maka akan terbukti bahwa sudut bersebrangan adalah sama besar.

4. Model C digunakan untuk mengetahui jumlah sudut-sudut yang sepihak adalah .

Ø Ambil model C lalu tempelkan pada papan Hubantsuka menggunakan paku. Letakkan model sedmikian sehingga garis-garis pada model dan papan Hubantsuka saling berhimpit.

Ø Perhatikan nama-nama sudut pada model C.

Ø Perhatikan sudut 2 dan sudut 3 yang sepihak, lalu putar searah atau berlawanan arah jarum jam sebesar akan terlihat bahwa sudut 2 dan sudut 3 mempunyai sudut berpelurus yaitu

Ø Lakukan hal yang sama pada sudut-sudut berikutnya.

Itulah sedikit pembahasan tentang alat peraga HUBANTSUKA dan cara pembuatannya. terimakasih kepada Rizqi Alfian Ardhany dan Arman yang telah berkontribusi dalam mewujudkan pembelajaran matematika yang asyik. semoga artikel ini bisa bermanfaat bagi teman-teman yang sedang mencari refrensi alat peraga yang akan di buat. salam hangat dari mimin yang jauh ini. uhhhhhh

Contoh Alat Peraga SMP dan Cara pembuatannya ; HUBANTSUKA ( Hubungan Antara Sudut Matematika )

Advertisement

1 Response to "Contoh Alat Peraga SMP dan Cara pembuatannya ; HUBANTSUKA ( Hubungan Antara Sudut Matematika )"