Diketahui bilangan 1,2,3,..,2010. ada berapa banyak bilangan tersebut yang dapat ditulis sebagai penjumlahan beberapa bilagan asli berurutan?
Diketahui bilangan 1,2,3,…,2010. Berapa banyak bilangan tersebut yang dapat ditulis sebagai penjumlahan beberapa bilangan asli.
Contoh:
5 = 2+3 dapat ditulis sebagai jumlah 2 bilangan
6 = 1+2+3 dapat ditulis sebagai jumlah 3 bilangan
jawab:
# cek beberapa bilangan
1 = tidak ada
2 = tidak ada
3 = 1+2
4 = tidak ada
5 = 2+3
6 = 1+2+3
7 = 3+4
8 = tidak ada
9 = 2+3+4 dan 4+5
10 = 1+2+3+4
11 = 5+6
12 = 3+4+5
13 = 6+7
14 = 2+3+4+5
15 = 7+8, 4+5+6, dan 1+2+3+4+5
16 = tidak ada
# dan hasil diatas diketahui pola bilangan yang tidak ada jumlah bilangan asli berurutan adalah 1,2,4,8,16,.... dapat dibuktikan sebagai berikut :
1+2+3+4+5+....
dari deret aritmatika (Sn) berlaku,
}{2} "Sn =\frac{n(a+Un)}{2}")
keterangan ; n = banyaknya bilangan
a = suku pertama
Un = suku terakhir
# Dalam barisan bilangan asli, kita bagi dalam beberapa kasus;
a). jika n = ganjil, maka kemungkinannya :
1. a genap dan Un genap, sehingga a+Un = genap
2. a ganjil dan Un ganjil, sehingga a+Un = genap
karena ( a+Un ) genap, maka n x ( a+Un ) = ganjil x genap
b). jika n = genap, maka kemungkinannya:
1. a genap dan Un ganjil, sehingga a+Un = ganjil
2. a ganjil dan Un genap, sehingga a+Un = ganjil
karena ( a+Un ) ganjil, maka n x ( a+Un 0 = genap x ganjil
# Dari uraian di atas dapat kita simpulkan bahwa;
n x ( a+Un ) selalu genp x ganjil
}{2},\text{maka&space;hasil} "\text{karena Sn}=\frac{n(a+Un)}{2},\text{maka hasil}")
Sn yang kemungkinan ada 2, yaitu ;
}{2},\text{hasilnya&space;genap}\\\text{b.&space;bilangan&space;ganjil&space;x&space;ganji,&space;jika}\frac{n(a+Un)}{2},\text{hasilnya&space;ganjil} "\\\text{a. bilangan ganjl x genap , jika}\frac{n(a+Un)}{2},\text{hasilnya genap}\\\text{b. bilangan ganjil x ganji, jika}\frac{n(a+Un)}{2},\text{hasilnya ganjil}")
Dari pertanyaan di atas yang tidak mungkin
Contoh:
5 = 2+3 dapat ditulis sebagai jumlah 2 bilangan
6 = 1+2+3 dapat ditulis sebagai jumlah 3 bilangan
jawab:
# cek beberapa bilangan
1 = tidak ada
2 = tidak ada
3 = 1+2
4 = tidak ada
5 = 2+3
6 = 1+2+3
7 = 3+4
8 = tidak ada
9 = 2+3+4 dan 4+5
10 = 1+2+3+4
11 = 5+6
12 = 3+4+5
13 = 6+7
14 = 2+3+4+5
15 = 7+8, 4+5+6, dan 1+2+3+4+5
16 = tidak ada
# dan hasil diatas diketahui pola bilangan yang tidak ada jumlah bilangan asli berurutan adalah 1,2,4,8,16,.... dapat dibuktikan sebagai berikut :
1+2+3+4+5+....
dari deret aritmatika (Sn) berlaku,
keterangan ; n = banyaknya bilangan
a = suku pertama
Un = suku terakhir
# Dalam barisan bilangan asli, kita bagi dalam beberapa kasus;
a). jika n = ganjil, maka kemungkinannya :
1. a genap dan Un genap, sehingga a+Un = genap
2. a ganjil dan Un ganjil, sehingga a+Un = genap
karena ( a+Un ) genap, maka n x ( a+Un ) = ganjil x genap
b). jika n = genap, maka kemungkinannya:
1. a genap dan Un ganjil, sehingga a+Un = ganjil
2. a ganjil dan Un genap, sehingga a+Un = ganjil
karena ( a+Un ) ganjil, maka n x ( a+Un 0 = genap x ganjil
# Dari uraian di atas dapat kita simpulkan bahwa;
n x ( a+Un ) selalu genp x ganjil
Sn yang kemungkinan ada 2, yaitu ;
Dari pertanyaan di atas yang tidak mungkin
memenuhi adalah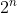 
, n bilangan cacah
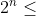2010. yaitu 1,2,4,8,16,32,64,128,256,512, 1024
( ada 11 bilangan ).
jadi, bilangan yang dapat ditulis sebagai penjumlahan beberapa bilangan asli ada 2010-11 = 1999 bilangan.
itulah sedikit pembahasan dari soal HOTS aritmatika, semoga bermanfaat ya teman-teman. salam hangat dari mimin
jadi, bilangan yang dapat ditulis sebagai penjumlahan beberapa bilangan asli ada 2010-11 = 1999 bilangan.
itulah sedikit pembahasan dari soal HOTS aritmatika, semoga bermanfaat ya teman-teman. salam hangat dari mimin
0 Response to "Diketahui bilangan 1,2,3,..,2010. ada berapa banyak bilangan tersebut yang dapat ditulis sebagai penjumlahan beberapa bilagan asli berurutan?"
Post a Comment