Diketahui fungsi g(x) = 1/3x³ - A²x + 7, A konstanta. Jika f(x) = g(2x + 1) dan f turun pada -3/2 < x < 1/2, nilai minimum relatif g adalah...
Diketahui fungsi g(x) = 1/3x³ - A²x + 7, A konstanta. Jika f(x) = g(2x + 1) dan f turun pada -3/2 < x < 1/2, nilai minimum relatif g adalah...
A. 4/3
B. 5/3
C. 2
D. 7/3
E. 8/3
Pembahasan :
Diketahui : g(x) = 1/3x³ - A²x + 7
f(x) = g(2x + 1)
f turun pada -3/2 < x < 1/2
Ditanyakan : Nilai minumum relatif g adalah...?
Jawab :
* Kita subsitusikan x = 2x + 1
f(x) = g(2x + 1)
= 1/3(2x + 1)³ - A²(2x + 1) + 7
f'(x) = 1/3 x 3(2x + 1)²(2) - A²(2)
= 2(2x + 1)² - 2A²
* Grafik fungsi f(x) turun pada interval -3/2 < x < 1/2,
berartif naik pada ( x < -3/2 atau x> 1/2), dan f stasioner
di x = -3/2 dan x = 1/2. karena f stasioner di x = -3/2 dan x = 1/2,
maka f'(-3/2) = 0 dan f'(1/2) = 0.
* Kita subsitusikan nilai x = 1/2.
f'(x) = 2(2x + 1)² - 2A²
0 = 2(2(1/2) + 1)² - 2A²
0 = 2(1 + 1)² - 2A²
0 = 2(2)² - 2A²
0 = 2(4) - 2A²
0 = 8 - 2A²
2A² = 8
A² = 8/2
A² = 4
* Kita subsitusikan nilai A² = 4 ke dalam fungsi g(x) dan g'(x).
Dengan demikian, diperoleh bahwa :
* g(x) = 1/3 x³ - A²x + 7
= 1/3 x³ - 4x + 7
* g'(x) = 1/3 x 3x² - 4
= x² - 4
* Menentukan nilai minimum relatif fungsi g.
fungsi g mencapai stasioner jika g'(x) = 0. Maka :
g'(x) = 0
x² - 4 = 0
(x + 2) (x - 2) = 0
x + 2 = 0 atau x - 2 = 0
x = -2 x = 2
* Diagram tanda nilai fungsi g'(x) di setiap nilai x adalah :
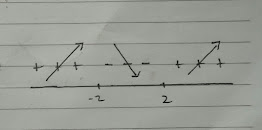
* Dari diagram tanda di atas, tanpakbahwa kurva g(x) mencapai minumum di x = 2.
Sehingga nilai minimum fungsi g(x) adalah
g = g(2)
= 1/3 x³ - 4x + 7
= 1/3 (2)³ - 4(2) + 7
= 1/3 x 8 - 8 + 7
= 8/3 - 1
= 8/3 - 3/3
= 5/3
Jadi, Nilai minumum relatif g adalah 5/3. Jawabannya ( B ).
Itulah pembahasan soal UN SMA tahun 2016 tentang materi fungsi kuadrat. Jika ada yang ingin ditanyakan atau didiskusikan perihal materi di atas, silahkan tinggalkan pesan di kolom komentar. Nuhun sewuuu...
0 Response to "Diketahui fungsi g(x) = 1/3x³ - A²x + 7, A konstanta. Jika f(x) = g(2x + 1) dan f turun pada -3/2 < x < 1/2, nilai minimum relatif g adalah..."
Post a Comment