Sebuah lingkaran berpusat di titik P(2, -3). Jika lingkaran tersebut menyinggung 12y = 5x - 7, persamaan lingkaran adalah...
Sebuah lingkaran berpusat di titik P(2, -3). Jika lingkaran tersebut menyinggung 12y = 5x - 7, persamaan lingkaran adalah...
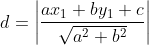
-12(-3)-7}{\sqrt{5^{2}+9-12^{2}}}&space;\right&space;|)
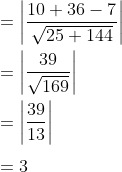
A. x² + y² - 4x + 6y + 4 = 0
B. x² + y² - 4x + 6y + 9 = 0
C. x² + y² - 4x + 6y + 22 = 0
D. x² + y² + 4x - 6y + 4 = 0
E. x² + y² + 4x - 6y + 22 = 0
Pembahasan :
Diketahui : Titik pusat = p(2, -3)
Garis singgung = 12y = 5x - 7
Ditanyakan : Persamaan lingkaran...?
Jawab :
* Rumus jarak titik (x1,y1) ke garis ax + by + c = 0 adalah :
* Jarak titik pusat (2, -3) ke garis 12y = 5x - 7 atau 5x - 12y - 7 = 0
merupakan jari-jari lingkaran, yaitu :
* Persamaan lingkaran berpusat di (a,b) dan berjari-jari r adalah :
(x - a)² + (y - b)² = r²
* Persamaan lingkaran berpusat di (2, -3) dan berjari-jari r = 3 adalah :
(x - a)² + (y - b)² = r²
(x - 2)² + (y -(-3))² = 3²
(x - 2)² + (y + 3)² = 3²
x² - 2(x)(2) + 2² + y² + 2(y)(3) + 3² = 3²
x² - 4x + 4 + y² + 6y + 9 = 9
x² + y² - 4x + 6y + 4 + 9 - 9 = 0
x² + y² - 4x + 6y + 4 = 0
Jadi, persamaan lingkarannya x² + y² - 4x + 6y + 4 = 0
Jawabannya ( A ).
Itulah pembahasan soal mengenai persamaan lingkaran yang mimin ambil dari soal UN SMA/SMK/MA tahun 2018. Semoga bermanfaat dan mudah untuk dipahami. Jika ada yang ingin ditanyakan atau didiskusikan perihal soal sejenis di atas, silahkan tinggalkan pesan di kolom komentar. Haturr nuhunnn..
0 Response to "Sebuah lingkaran berpusat di titik P(2, -3). Jika lingkaran tersebut menyinggung 12y = 5x - 7, persamaan lingkaran adalah..."
Post a Comment