Diketahui fungsi g(x) = - 1/9 x³ + A²x + 1 dan A konstanta. Jika f(x) = g(x + 2) dan fungsi f(x) naik pada interval - 5 < x < 1, nilai minimum fungsi g(x) adalah...
Diketahui fungsi g(x) = - 1/9 x³ + A²x + 1 dan A konstanta. Jika f(x) = g(x + 2) dan fungsi f(x) naik pada interval - 5 < x < 1, nilai minimum fungsi g(x) adalah...
A. 11
B. 7
C. 5
D. -5
E. -7
Pembahasan :
Diketahui :
g(x) = - 1/9 x³ + A²x + 1
A = konstanta
f(x) = g(x + 2)
f(x) naik pada interval - 5 < x < 1
Ditanyakan : nilai minimum fungsi g(x) adalah...?
Jawab :
* Kita subsitusikan f(x) = g(x + 2), maka :
f(x) = g(x + 2)
= - 1/9 (x + 2)³ + A²(x + 2) + 1
* Selanjutnya kita cari turunan pertama dari f(x)
f(x) = - 1/9 (x + 2)³ + A²(x + 2) + 1
f'(x) = -3/9 (x + 2)² + A²
= - 1/3 (x + 2)² + A²
* f(x) naik pada interval -5 < x < 1, berarti f(x) turun pada x < - 5
dan x > 1 serta f(x) stasioner di x = - 5 dan x = 1.
* Oleh karena f(x) stasioner di x = -5 dan x = 1,
maka f'(-5) = 0 dan f'(1) = 0.
Kita ambil yang x = 1. Maka :
f'(x) = - 1/3 (x + 2)² + A²
0 = - 1/3 (1 + 2)² + A²
0 = - 1/3 (3)² + A²
0 = - 1/3 (9) + A²
0 = -3 + A²
3 = A²
Dengan demikian , diperoleh fungsi g(x) = - 1/9 x³ + 3x + 1
* Kita turunkan fungsi g(x) ke turunan pertama, maka :
g(x) = - 1/9 x³ + 3x + 1
g'(x) = -3/9 x² + 3
= - 1/3 x² + 3
* Fungsi g(x) mencapai stasioner jika g'(x) = 0, maka :
g'(x) = - 1/3 x² + 3
0 = - 1/3 x² + 3 (kalikan dengan 3)
0 = -x² + 9
x² = 9
x² - 9 = 0
(x - 3) (x + 3) = 0
x - 3 = 0 atau x + 3 = 0
x = 3 x = - 3
* Kita buat diagram tanda g'(x) = - 1/3 x² + 3 adalah :
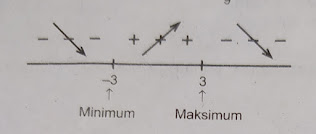
* Dari diagram tanda di atas nampak bahwa fungsi g(x) mencapai minimum di x = - 3.
Sehingga :
Nilai minimun fungsi g(x) = g(-3)
g(x) = - 1/9 x³ + 3x + 1
g(-3) = - 1/9 (-3)³ + 3(-3) + 1
= - 1/9 ( -27) + (-9) + 1
= 3 - 9 + 1
= - 5
Jadi, nilai minimum fungsi g(x) adalah - 5. Jawabannya ( D ).
Itulah pembahasan soal UN SMA tahun 2018 mengenai turunan fungsi. Semoga bermanfaat dan mudah untuk dipahami. Tetap semangat dan santuy dalam melaksanakan tugas-tuganya yah temen. Jika ada yang ingin ditanyakan atau didiskusikan perihal soal sejenis, silahkan tinggalkan pesan di kolom komentar. Terima kasihh temen-temen.
0 Response to "Diketahui fungsi g(x) = - 1/9 x³ + A²x + 1 dan A konstanta. Jika f(x) = g(x + 2) dan fungsi f(x) naik pada interval - 5 < x < 1, nilai minimum fungsi g(x) adalah..."
Post a Comment