Diketahui segitiga ABC dengan panjang BC =12 cm dan besar < ABC = 60°. Jika luas ∆ABC = 24√3 cm², panjang sisi AC =...

Diketahui segitiga ABC dengan panjang BC =12 cm dan besar < ABC = 60°. Jika luas ∆ABC = 24√3 cm², panjang sisi AC =...

A. 2√7 cm

B. 8 cm

C. 4√7 cm

D. 12 cm

E. 6√5 cm

Pembahasan :

Diketahui :

panjang BC =12 cm

 < ABC = 60°

luas ∆ABC = 24√3 cm²

Ditanyakan : Panjang AC adalah...?

Jawab :

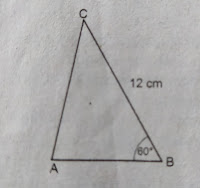
* Kita ilustrasikan soal kedalam gambar

* Kita menggunakan aturan sinus karena akan mencari panjang AC, maka :

L.ABC = 24√3 

1/2 x AB x BC x sin < ABC = 24√3

1/2 x AB x 12 x sin 60° = 24√3

1/2 x AB x 12 x 1/2 √3 = 24√3

3√3 x AB = 24√3

AB = 24√3 / 3√3

AB = 8 cm

* Selanjutnya kita gunakan aturan kosinus, maka : 

AC² = AB² + BC² - 2.AB.BC x cos <ABC 

        = 8² + 12² - 2.8.12 x cos 60° 

        = 64 + 144 - 16.12 x 1/2

        = 208 - 16.6

        = 208 - 96

        = 112

AC = √112

AC = √(16 x 7)

AC = 4√7 cm

Jadi, panjang AC adalah 4√7 cm. Jawabannya ( C ).

Itulah pembahasan soal mengenai materi rumus sinus dan kosinus. Semoga bermanfaat dan mudah untuk dipahami. Pesan mimin untuk temen-temen, jangan sampe ketuker yah rumus sinus dan kosinusnya. Good luck and God bless for you. Thank you

Advertisement

Subscribe to receive free email updates: