Grafik fungsi kuadrat f(x) = 2x² + (p - 1)x - 14 mempunyai sumbu simetris x = -3. Koordinat titik balik fungsi tersebut adalah...
Grafik fungsi kuadrat f(x) = 2x² + (p - 1)x - 14 mempunyai sumbu simetris x = -3. Koordinat titik balik fungsi tersebut adalah...
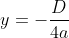
}{4.2}\\\\=-\frac{144+112}{8}\\\\=-\frac{256}{8}\\\\=-32)
A. (-3, - 32)
B. (-3, - 28)
C. (-3, - 14)
D. (-3, 14)
E. (-3, 32)
Pembahasan :
Diketahui :
f(x) = 2x² + (p - 1)x - 14
a = 2
b = (p - 1)
c = -14
umbu simetris x = -3
Ditanyakan : Koordinat titik balik fungsi tersebut adalah...?
Jawab :
* Karena persamaan sumbu simetri adalah x = -3. Maka kita dapat mencari nilai p :
x = - 3
-b / 2a = -3
-(p - 1) / 2.2 = - 3
-(p - 1) / 4 = - 3
-(p - 1) = - 3 x 4
-p + 1 = - 12
-p = - 12 - 1
- p = - 13
p = 13
* Kita subsitusikan nilai p = 13 ke persamaan fungsi kuadratnya, maka :
f(x) = 2x² + (p - 1)x - 14
= 2x² + (13 - 1)x - 14
= 2x² + 12x - 14
maka dapat kita ketahui bahwa nilai :
a = 2
b = 12
c = - 14
* Dengan begitu maka titik puncaknya adalah :
x = - 3
Jadi, koordinat titik baliknya adalah (-3, - 32). Jawabannya ( A ).
Itulah pembahasan soal mengenai persamaan fungsi kuadrat yang mencari koordinat titik baliknya. Semoga bermanfaat dan mudah untuk dipahami. Jika ada yang ingin ditanyakan atau didiskusikan perihal materi atau soal di atas, silahkan tinggalkan pesan di kolom komentar. Innsyaaloh mimin akan membantu jika di rasa masih bisa. Terima kasih dulur kabehh.
0 Response to "Grafik fungsi kuadrat f(x) = 2x² + (p - 1)x - 14 mempunyai sumbu simetris x = -3. Koordinat titik balik fungsi tersebut adalah..."
Post a Comment