Diketahui T.ABC adalah limas segitiga beraturan dengan panjang rusuk alas 12 cm dan panjang rusuk tengah 6√2 cm, serta titik E di tengah rusuk TC. Hitunglah jarak titik A ke rusuk BE....
Diketahui T.ABC adalah limas segitiga beraturan dengan panjang rusuk alas 12 cm dan panjang rusuk tengah 6√2 cm, serta titik E di tengah rusuk TC. Hitunglah jarak titik A ke rusuk BE....
Pembahasan :
Diketahui :
panjang rusuk alas 12 cm
panjang rusuk tengah 6√2 cm
titik E di tengah rusuk TC
Ditanyakan : jarak titik A ke rusuk BE...?
Jawab :
Kita ilustrasikan soal ke dalam gambar


Dari gambar di atas, kita ambil segitiga BCT.

Kita cari panjang TO, maka :
TO = √(BT² - BO²)
= √((6√2)² - (6)²)
= √((36.2) - (36))
= √(72 - 36)
= √36
= 6 cm
Selanjutnya kita ambil segitiga ABE.
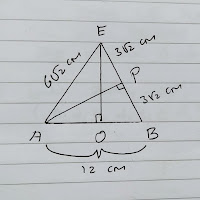
Dari gambar di atas, kita cari panjang EO, maka :
EO = √(AE² - AO²)
= √(6√2)² - (6)²)
= √(36.2 - 36)
= √(72 - 36)
= √36
= 6 cm
Kita cari panjang BE dengan membandingkan luas dua segitiga, yaitu L.segitiga BTC = L.segitiga TBC. Maka :
1/2 x BC x TO = 1/2 x TC x BE
BC x TO = TC x BE
12 x 6 = 6√2 x BE
72 = 6√2 x BE
72 / 6√2 = BE
(72√2)/12 = BE
6√2 = BE
panjang BE = AE = 6√2 cm.
Setelah kita mengetahui panjang BE = AE = 6√2 cm, maka kita bisa mencari panjang AP dengan membandingkan luas kedua segitiga.
L.segitiga AEB = L.segitiga EAB
1/2 x AB x EO = 1/2 x BE x AP
AB x EO = BE x AP
12 x 6 = 6√2 x AP
72 = 6√2 x AP
72 / 6√2 = AP
(72√2 / 12) = AP
6√2 = AP
Jadi, jarak titik A ke rusuk BE adalah 6√2 cm.
Itulah pembahasan contoh soal mengenai materi bangun ruang limas segitiga beraturan. Semoga bermanfaat dan mudah untuk dipahami yahh. Tetap semangat dalam menggapai cita-cita yang temen-temen inginkan. Terima kasih semua...
Bagaimana penjelasan anda bahwa BE adalah garis tinggi?
ReplyDeleteSedangkan E adalah titik tengah TC, sehingga BE adalah garis berat..
Dan garis berat belum tentu membentuk sudut siku-siku.. Sehingga tidak bisa diasumsikan sebagai garis tinggi segitiga TBC.
Tolong penjelasannya