Diketahui titik A(-2,-1), B(2,-1), C(3,4), dan D(-1,4). Segi empat ABCD dirotasikan 180° dengan pusat O(0,0), lalu ditransformasikan oleh matriks (3 2 1 -2). Luas bayangannya adalah..
Diketahui titik A(-2,-1), B(2,-1), C(3,4), dan D(-1,4). Segi empat ABCD dirotasikan 180° dengan pusat O(0,0), lalu ditransformasikan oleh matriks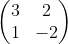 
. Luas bayangannya adalah...
A. 20 satuan luas
B. 40 satuan luas
C. 80 satuan luas
D. 120 satuan luas
E. 160 satuan luas
Pembahasan :
Diketahui :
titik A(-2,-1)
titik B(2,-1)
titik C(3,4)
titik D(-1,4)
dirotasikan dengan 180°
pusat O(0,0)
ditransformasikan oleh matriks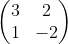
Ditanyakan : Luas bayangannya segi empat ABCD adalah...
Jawab :
Kita ilustrasikan titik-titik itu ke dalam bidang cartesius, yaitu akan terbentuk bangun datar segi empat ABCD.
Dari gambar dapat kita ketahui bahwa bangun
datar segi empat itu berbentuk jajaran genjang.
alas = AB = 4 satuan
tinggi = 5 satuan
Kita cari luas bangun datar ABCD tersebut.
L ABCD = alas x tinggi
= 4 x 5
= 20 satuan luas
Karena rotasi tidak mengubah ukuran luas bangun datar ABCD, maka rotasi 180° dengan pusat O(0,00 dalam perhitungan luas bayangannya dapat kita abaikan.
Selanjutnya kita akan mencari luas bayangan segi empat ABCD oleh transformasi matriks M = 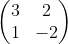dapat dihitung sebagai berikut :
Det (M) =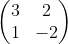
= - 6 - 2
= - 8
Luas bayangan segi empat ABCD adalah :
L' = |det (M)| x L
= |-8| x 20
= 160 satuan luas
Jadi, Luas bayangannya segi empat ABCD adalah 160 satuan luas. Jawabannya ( E ).
Itulah pembahasan contoh soal mengenai geometeri transformasi yang mimin ambil dari soal latihan UNBK tahun 2019. Semoga bermanfaat dan mudah untuk dipahami yahh. Semangat temen-temen dalam hal belajar. Terima kasihhh.
0 Response to "Diketahui titik A(-2,-1), B(2,-1), C(3,4), dan D(-1,4). Segi empat ABCD dirotasikan 180° dengan pusat O(0,0), lalu ditransformasikan oleh matriks (3 2 1 -2). Luas bayangannya adalah.."
Post a Comment