Johan berlatih memasukan bola ke dalam ring basket dengan pelemparan berulang-ulang. Peluang bola masuk ke ring basket 3/5. Jika Johan melemparkan bola sebanyak 4 kali, peluang bola masuk ke ring basket sebanyak 3 kali sebesar...

Johan berlatih memasukan bola ke dalam ring basket dengan pelemparan berulang-ulang. Peluang bola masuk ke ring basket 3/5. Jika Johan melemparkan bola sebanyak 4 kali, peluang bola masuk ke ring basket sebanyak 3 kali sebesar...

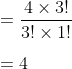
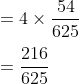
A. 18/125

B. 24/125

C. 36/125

D. 216/625

E. 72/125

Pembahasan :

Diketahui : 

Peluang bola masuk = P(G) = 3/5

Banayk percobaan = 4 kali

Ditanyakan : peluang bola masuk ke ring basket sebanyak 3 kali sebesar...?

Jawab :

Cara I Cabi (Cara Biasa) :

Kita cari terlebih dahulu peluang bola tidak masuk.:

Peluang bola tidak masuk = P(T)

P(T) = 1 - P(G)

        = 1 - 3/5

        = 5/5 - 3/5

        = 2/5

Terdapat 4 kemungkinan kejadian terjadinya 3 kali bola masuk ring basket dari 4 kali pelemparan bola. Secara lengkap 4 kejadian tersebut dapat ditanyakan dengan urutan seperti berikut :

Kejadian	Lemparan Bola
	I	II	III	IV
K1	G1	G2	G3	T4
K2	G1	G2	T3	G4
K3	G1	T2	G3	G4
K4	T1	G2	G3	G4

Keterangan :

K1 = Kejadian bola masuk ke ring basket pada 

         pelemparan I, II, III, dan bola tidal masuk 

         ring basket pada pelemparan ke IV

      = {G1, G2, G3, T4}

Antara kejadian G1, G2, G3, dan T4 saling bebas, 

sehingga :

P(K1) = P(G1) x P(G2) x P(G3) x P(T4)

           = 3/5 x 3/5 x 3/5 x 2/5

           = 54/625

K2 = Kejadian bola masuk ke ring basket 

         pada pelemparan I, II, IV dan bola tidak 

         masuk ring basket pada pelemparan III.

      = {G1, G2, T3, G4}

Antara kejadian G1, G2, T3, dan G4 saling bebas, 

sehingga :

P(K2) = P(G1) x P(G2) x P(T3) x P(G4)

           = 3/5 x 3/5 x 2/5 x 3/5

           = 54/625

Dengan cara sama seperti menentukan nilai 

P(K1) dan P(K2) diperoleh nilai :

P(K3 = P(K4) = 54/625

Antara kejadian K1, K2, K3, dan K4 saling bebas sehinga peluang 3 kali bola masuk ke ring basket dari  4 pelemparan bola :

P = P(K1) + P(K2) + P(K3) + P(K4)

   = 54/625 + 54/625 + 54/625 + 54/625

   = 216 / 625

Cara II Cadas ( Cara Cerdas ) :

Cara menentukan urutan 3 kali bola masuk ring basket dari 4 kali pelemparan bola sama dengan cara menempatkan 3 huruf G pada 4 tempat. 

Cara menempatkan 3 huruf G pada 4 tempat merupakan permasalahan kombinasi.

Sehingga banyak cara menempatkan 3 huruf G pada 4 tempat adalah :

 

        

Peluang 3 kali bola masuk ke ring basket dan 1 kali bola tidak masuk ring basket :

P(3G,1T) = (P(G))³ + P(T)

                = (3/5)³ + (2/5)

                = 27/125 + 2/5

                = 54/625

Peluang 3 kali bola masuk ke ring basket dari 4 kali pelemparan adalah :

 

     

Jadi, peluang bola masuk ke ring basjet 

sebanyak 3 kali sebesar 216/625. Jawabannya ( D ).

Itulah contoh soal pembahasan mengenai materi kaidah pencacahan yang mimin ambil dari soal latihan UNBK SMA tahun 2019. Semoga bermanfaat dan mudah untuk dipahami yahh. Tetap semangat dalam belajar dan selalu berusaha menebar kebaikan. Terima kasih temen temen..

Advertisement

Subscribe to receive free email updates: