Suatu deret aritmatika mempunyai suku ke-4 bernilai 13 dan suku ke-9 bernilai 28. Jumlah dua puluh suku pertama deret tersebut adalah
Suatu deret aritmatika mempunyai suku ke-4 bernilai 13 dan suku ke-9 bernilai 28. Jumlah dua puluh suku pertama deret tersebut adalah . . .
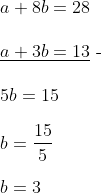
A. 620
B. 650
C. 680
D 710
E. 720
Pembahasan :
Diketahui :
Nilai Suku ke-4 = 13
Nilai Suku ke-9 = 28
Ditanyakan : Jumlah dua puluh suku pertama deret tersebut adalah . . .?
Jawab :
Ingat :
Rumus suku ke-n :
Un = a + (n - 1)b
Sehingga kita peroleh :
U4 = a + (4 - 1)b
13 = a + 3b . . . persamaan (1)
U9 = a + (9 - 1)b
28 = a + 8b . . . persamaan (2)
Selanjutnya kita eliminasi pers (1) dan (2)
Subsitusikan nilai b = 3 ke persamaan (1)
a + 3b = 13
a + 3(3) = 13
a + 9 = 13
a = 13 - 9
a = 4
Kita peroleh nilai a = 4 dan b = 3.
Rumus jumlah n suku pertama deret aritmatika adalah :
Sn = n/2 (2a + (n - 1)b)
Maka jumlah dua puluh suku pertama :
Sn = n/2 (2a + (n - 1)b)
S20 = 20/2 (2(4) + (20 - 1)3)
= 10 (8 + (19 x 3))
= 10 ( 8 + 57)
= 10 (65)
= 650
Jadi, Jumlah dua puluh suku pertama deret tersebut adalah 650.
Jawabannya ( B ).
Itulah pembahasan contoh soal mengenai materi barisan dan deret aritmatika, semoga bermanfaat dan mudah untuk dipahami yahh. Jangan lupa bernafas untuk pekerjaan hari ini, esok, dan lusa. Semangat temen-temen. Terima kasih.
0 Response to "Suatu deret aritmatika mempunyai suku ke-4 bernilai 13 dan suku ke-9 bernilai 28. Jumlah dua puluh suku pertama deret tersebut adalah "
Post a Comment