Persamaan garis dibawah ini yang tegak lurus dengan garis yang melalui titik P(-3, 8) dan Q(2, 5) adalah

Persamaan garis dibawah ini yang tegak lurus dengan garis yang melalui titik P(-3, 8) dan Q(2, 5) adalah . . .

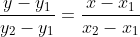
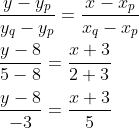
A. 3x - 5y - 14 = 0

B. 3x + 5y + 14 = 0

C. 5x + 3y - 42 = 0

D. 5x - 3y - 42 = 0

Pembahasan :

Diketahui :

Titik P = (-3, 8)

Titik Q = (2, 5)

Persamaan garisnya tegak lurus.

Ditanyakan : Persamaan garis yang melalui titik tersebut adalah . . .?

Jawab :

Ingat :

a. Persamaan garis yang melalui dua buah titik :

  

b. Persamaan garis melalui sebuah titik 

    dan bergardien m :

 

   y - y1 = m(x - x1)

c. Gardien garis :

    g ; ax + by + c = 0

    m = - a/b

d. Gardien dari kedua ruas garis yang saling 

    tegak lurus :

    m1 . m2 = -1

Maka : 

Persamaan garis yang tegak lurus dengan garis yang melalui titik P(-3, 8) dan Q(2, 5) adalah :

 

5(y - 8) = -3(x + 3)

5y - 40 = -3x - 9

3x + 5y - 40 + 9 = 0

3x + 5y - 31 = 0

Jadi, gardien persamaan di atas adalah :

m1 = - a/b

      = - 3/5

Karena tegak lurus, maka :

m1 . m2 = - 1

(- 3/5) . m2 = - 1

m2 = - 1 x (- 5/3)

m2 = 5/3

Pilih salah satu titik, misal Q(2 , 5), sehingga persamaan garis tersebut adalah :

y - 5 = m(x - x1)

y - 5 = 5/3   (x - 2)   (semua ruas dikali 3)

3y - 15 = 5 (x - 2)

3y - 15 = 5x - 10

5x - 3y + 15 - 10 = 0

5x - 3y +  5 = 0

Jadi, Persamaan garis yang melalui titik tersebut adalah 5x - 3y +  5 = 0.

Jawabannya ( D ).

Itulah pembahasan contoh soal mengenai materi persamaan garis lurs, semoga bermanfaat dan mudah untuk dipahami yah. Semangat dan semangat buat kalian yang senantiasa terus belajar, kejarlah angin hingga orang-orang disekitar tidak menyadari bahwa anda sudah jalan ke depan. Terima kasih semua.

Advertisement

Subscribe to receive free email updates: